Locally
Fortran 77 (f77), Fortran 90 (f90),
and Fortran 95 (f95), are all available on our workstations.
Both the workstations and the
file servers are from Sun.
Previously we used Digital Equipment computers.
This Appendix with Computer Exercises is also
available in Swedish
These computer exercises are small variants of those used at the teaching of Fortran at Linköping University, both for the students of technology and for the students in the mathematics and science program.
When I write course directory below it is intended as an advice to the local teacher to make the required files available to the students. Of course, it is also possible to type them from the textbook, extract them from this HTML-file, or get them electronically from our course directory. Using UNIX it is easy to introduce symbolic names, so the course directory $KURSBIB is /mailocal/lab/numt/TANA70/
Locally
Fortran 77 (f77), Fortran 90 (f90),
and Fortran 95 (f95), are all available on our workstations.
Both the workstations and the
file servers are from Sun.
Previously we used Digital Equipment computers.
Further information on the course (including experiences from earlier students) is available (mainly in Swedish) on URL=http://www.mai.liu.se/~boein/kurser/TANA70/
The computers used for teaching at the Department of Mathematics have been replaced during 2001, from DEC machines to Sun machines. The new computers also mean a change in location of the course directory. You define the course directory by writing
setenv KURSBIB /mailocal/lab/numt/TANA70/A suitable environment is obtained with the TANA70setup command.
Further information on the Sun Fortran 90, and its system parameters, and hints on compilation are available.
Further information on the DEC Fortran 90, and its system parameters, hints on compilation, and some examples are still available.
The following material shall be handed to the teacher:
Number of steps Step length
1 1
2 0.5
4 0.25
8 0.125
For those who do not know Pascal the recommended alternative is to get an
elementary textbook on numerical methods and code Runge-Kutta directly in Fortran.
The task is to solve the differential equation y'(x) = x2 + sin(xy) with the Runge-Kutta method, using the initial value y(1) = 2 going to x = 2 and using the step sizes above. The formulas for the Runge-Kutta method are for example in the description of exercise 8.
program RK1;
(* A simple program in Pascal for Runge-Kutta's method for a
first order differential equation.
dy/dx = x^2 + sin(xy)
y(1) = 2 *)
var number, i : integer;
h, k1, k2, k3, k4, x, y : real;
function f(x,y : real) : real;
begin
f := x*x + sin(x*y)
end;
begin
number := 1;
while number > 0 do
begin
x := 1.0;
y := 2.0;
writeln(' Give the number of steps ');
read(number);
if number >= 1 then
begin
writeln(' Give the step length ');
read(h);
writeln(' x y');
writeln(x, y);
for i := 1 to number do
begin
k1 := h*f(x,y);
k2 := h*f(x+0.5*h,y+0.5*k1);
k3 := h*f(x+0.5*h,y+0.5*k2);
k4 := h*f(x+h,y+k3);
x := x + h;
y := y + (k1+2*k2+2*k3+k4)/6;
writeln(x, y);
end;
end;
end;
end.
If you wish to run this program you have to replace the first line
program RK1;with the following extended line
program RK1(INPUT, OUTPUT);when running on a DEC UNIX system, but not on a Sun Solaris system.
When the program is believed to be correct (test with the equation x*x + 2 = 0), the second assignment is to modify the program so that it can accept data from either the keyboard or from a file $KURSBIB/lab21.dat. The modifications are required to be done in such a way that the user can select if data are supposed to be input directly from the keyboard or from a file, in which case the user also will be required to give the name of the file.
Finally, check that the program also works for the file $KURSBIB/lab22.dat.
Note that the program uses complex numbers, and that such values are input as pairs within parenthesis.
The program is also available in free mode Fortran 90 as $KURSBIB/lab2_e.f90.
The following material shall be handed to the teacher:
******************************************************************************
** This program calculates all roots (real and/or complex) to an **
** N:th-degree polynomial with complex coefficients. (N <= 10) **
** **
** n n-1 **
** P(z) = a z + a z + ... + a z + a **
** n n-1 1 0 **
** **
** The execution terminates if **
** **
** 1) Abs (Z1-Z0) < EPS ==> Root found = Z1 **
** 2) ITER > MAX ==> Slow convergence **
** **
** The program sets EPS to 1.0E-7 and MAX to 30 **
** **
** The NEWTON-RAPHSON method is used: z1 = z0 - P(z0)/P'(z0) **
** The values of P(z0) and P'(z0) are calculated with HORNER'S SCHEME. **
** **
** The array A(0:10) contains the complex coefficients of the **
** polynomial P(z). **
** The array B(1:10) contains the complex coefficients of the **
** polynomial Q(z), **
** where P(Z) = (z-z0)*Q(z) + P(z0) **
** The coefficients to Q(z) are calculated with HORNER'S SCHEME. **
** **
** When the first root has been obtained with the NEWTON-RAPHSON **
** method, it is divided away (deflation). **
** The quotient polynomial is Q(z). **
** The process is repeated, now using the coefficients of Q(z) as **
** input data. **
** As a starting approximation the value STARTV = 1+i is used **
** in all cases. **
** Z0 is the previous approximation to the root. **
** Z1 is the latest approximation to the root. **
** F0 = P(Z0) **
** FPRIM0 = P'(Z0) **
******************************************************************************
COMPLEX A(0:10), B(1:10), Z0, Z1, STARTV
INTEGER N, I, ITER, MAX
REAL EPS
DATA EPS/1E-7/, MAX /30/, STARTV /(1,1)/
******************************************************************************
20 WRITE(6,*) 'Give the degree of the polynomial'
READ (5,*) N
IF (N .GT. 10) THEN
WRITE(6,*) 'The polynomial degree is maximum 10'
GOTO 20
WRITE (6,*) 'Give the coefficients of the polynomial,',
, ' as complex constants'
WRITE (6,*) 'Highest degree coefficient first'
DO 30 I = N, 0, -1
WRITE (6,*) 'A(' , I, ') = '
READ (5,*) A(I)
30 CONTINUE
WRITE (5,*) ' The roots are',' Number of iterations'
******************************************************************************
40 IF (N GT 0) THEN
C ****** Find the next root ******
Z0 = (0,0)
ITER = 0
Z1 = STARTV
50 IF (ABS(Z1-Z0) .GE. EPS) THEN
C ++++++ Continue the iteration until two estimates ++++++
C ++++++ are sufficiently close. ++++++
ITER = ITER + 1
IF (ITER .GT. MAX) THEN
C ------ Too many iterations ==> TERMINATE ------
WRITE (6,*) 'Too many iterations.'
WRITE (6,*) 'The latest approximation to the root is ',Z1
GOTO 200
ENDIF
Z0 = Z1
HORNER (N, A, B, Z0, F0, FPRIM0)
C ++++++ NEWTON-RAPHSON'S METHOD ++++++
Z1 = Z0 - F0/FPRIM0
GOTO 50
ENDIF
C ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
100 WRITE (6,*) Z1, ' ',Iter
C ****** The root is found. Divide it away and seek the next one *****
N = N - 1
FOR I = 0 TO N DO
A(I) = B(I+1)
GOTO 40
ENDIF
200 END
SUBROUTINE HORNER(N, A, B, Z, F, FPRIM)
****** For the meaning of the parameters - see the main program ******
****** BI and CI are temporary variable. ******
INTEGER N, I
COMPLEX A(1:10), B(0:10), Z, F, FPRIM, BI, CI
BI = A(N)
B(N) = BI
CI = BI
DO 60 I = N-1, 1, -1
BI = A(I) + Z*BI
CI = BI + Z*CI
B(I) = BI
C ++++++ BI = B(I) for the calculation of P(Z) ++++++
C ++++++ CI for the calculation of P'(Z) ++++++
60 CONTINUE
F = A(0) + Z*BI
FPRIM = CI
RETURN
END
****** END HORNER'S SCHEME ******
****** This program is composed by Ulla Ouchterlony 1984 ******
****** The program is translated by Bo Einarsson 1995 ******
Comments. I recommend the following process at the solution of this exercise.
f77 -u lab2_e.f
a.out
Using a modern system, for example Fortran 90, you put the statement
IMPLICIT NONE first in booth the main program and the subroutine.
The command -u has another meaning on the Absoft compiler.
f77 -C lab2_e.f
a.out
With the Absoft compiler you write f90 -Rb and with
the Intel ifort 8.0 you write ifort -CB.
The explicit DO-loop below will write seven lines, each one with one value of X
DO I = 1, 13, 2 WRITE(*,*) X(I) END DO
The implicit DO-loop below will write only one line, but with seven values of X
WRITE(*,*) ( X(I), I = 1, 13, 2)
I recommend that you test if your system permits this simplified form for input, but please use it only for input via the keyboard and never at input from a file (of portability reasons).
Make a test run and print a table with x and J0(x) for x = 0.0, 0.1, ... 1.0. Make the output to look nice!
At the use of the NAG Fortran 77 library the NAG User Notes are very useful. They describe the system specific parts of the library.
The required Bessel function in the NAG library is S17AEF and has the arguments X and IFAIL and in this order, where X is the argument for the Bessel function in single or double precision, and where IFAIL is an error parameter (integer). The error parameter is given the value 1 before entry, and is checked at exit. If it is 0 at exit, everything is OK, if it is 1 at exit, the magnitude of the argument is too large.
If the NAG library is installed in the normal way it is linked with the command
f77 prog.f -lnag
where prog.f is your program.
It is also permitted to use the new NAG Fortran 90 library. Please note that the functions have different names in this library (our Bessel function is nag_bessel_j0), and is linked with
f90 prog.f90 -lnagfl90
The error handling is done differently in the NAG Fortran 90 library,
there is no IFAIL parameter. For this exercise you may ignore
the error handling if you use this library. If an error occurs, it will
be automatically signalled.
If you use Fortran 90 for your own program but has the NAG library available only in Fortran 77 special care is necessary, see chapter 15, Method 2.
On Sun you compile and link with
f90 prog.f -lnag -lF77
and on DEC ULTRIX with
f90 prog.f -lnag -lfor -lutil -li -lots
On DEC UNIX -lfor -lutil -lots are available.
It is very important to note in which precision the NAG library is made available on your system. Using the wrong precision will usually give completely wrong results!
Local information:
The NAG library is not available on the Sun system in Linköping.
Write a program in Fortran 77 for tabulating the Bosse function Bo(x). Write the main program in such a way that it asks for an interval for which the function values are to be evaluated.
Make a test run and print a table with x and Bo(x) for x = 0.0, 0.1, ... 1.0. Make the output to look nice! Investigate also what happens with the arguments +800 and -900!
The Bosse function BO is in the library libbosse.a on the course directory and has the arguments X and IFAIL and in this order, where X is the argument for the Bosse function in single or double precision, and where IFAIL is an error parameter (integer). The error parameter is given the value 1 before entry, and is checked at exit. If it is 0 at exit, everything is OK, if it is 1 at exit, the argument is too large, if it is 2 at exit, the argument is too small. If the error parameter is zero on entry and an error occurs the program will stop with an error message from the library error handling subroutine, and not return to the user's program. The error handling is similar to the one in the NAG Fortran 77 library.
If the Bosse library is installed in the normal way it is linked with the command
f77 prog.f -L$KURSBIB -lbosse
where prog.f is your program.
If you use Fortran 90 for your own program but you still have the Bosse library available only in Fortran 77 special care is necessary, see chapter 15, Method 2, see also the discussion above in exercise 3b.
To make life simpler we have however made also a Fortran 90 version of the Bosse library, which is used with
f90 prog.f90 -L$KURSBIB -lbosse90
Remark 1. It is worthwhile to note that on some systems the order
of the directory and the library has to be reversed, as in
f90 prog.f90 -lbosse90 -L$KURSBIB
Remark 2. It is very important to note in which precision the Bosse library is made available on your system. Using the wrong precision will usually give completely wrong results!
Local information:
The Bosse library is in double precision on the Sun system.
Compare with Exercise 3 a.
y'(t) = z(t) y(0) = 1
z'(t) = 2*y*(1+y^2) + t*sin(z) z(0) = 2
Calculate an approximation to y(0.2) using the step size 0.04.
Repeat the calculation with the step sizes 0.02 and 0.01.
The functions representing the differential functions are to be given as
internal functions. It is therefore not permitted (in this exercise)
to use the usual external functions.
Starting values of t, y and z are to be given interactively, as well as the step size h.
Note that the requirement not to use external functions makes it a little more difficult to use a subprogram for the Runge-Kutta steps (in this case also the subprogram has to be internal). The aim of this requirement is to give the student an opportunity to use the new internal functions of Fortran 90.
The formulas for Runge-Kutta at systems are available here as an dvi-file and here as an HTML-file (which requires indices)! November 29
Remarks:
The first subprogram LASMAT is used to interactively input the floating point values of a quadratic matrix. The subprogram is required to ask for the dimension and give the user the choice of providing from the keyboard either all the values of the matrix, or only those which are different from zero, The matrix shall then be stored in a file, using maximal accuracy and minimal storage space. The possible sparsity of the matrix is however not permitted to be exploited at this storage process. The subprogram shall ask for the name of the file, but the file type (extension) will be .mat. The user is not permitted to give the file type.
Remarks to LASMAT:
The second subprogram LASVEK is used to interactively input the floating point values of a vector. The subprogram is required to ask for the dimension and give the user the choice of providing from the keyboard either all the values of the vector, or only those which are different from zero, The vector shall then be stored in a file, using maximal accuracy and minimal storage space. The possible sparsity of the vector is however not permitted to be exploited at this storage process. The subprogram shall ask for the name of the file, but the file type (extension) will be .vek. The user is not permitted to give the file type.
The third subprogram MATIN reads a matrix from the file with the given name and stores it as an array (matrix) in the subprogram, in such a way that the matrix is available also in the calling subprogram. The user is not permitted to give the file type.
The fourth subprogram VEKIN reads a vector from the file with the given name and stores it as an array (vector) in the subprogram in such a way that the vector is available also in the calling subprogram. The user is not permitted to give the file type.
The fifth subprogram MATUT prints a matrix on paper, with rows and columns in the normal way if the dimension is at most 10, and in an easily understandable way if the dimension is larger than 10. The available 132 positions of a typical line printer are to be utilized as well as possible. Output on paper is under UNIX not done directly, so you will have to first write to a file, which is then moved to paper with the UNIX print command lpr. Also using Microsoft Windows you create a text file which is then written by a Windows command.
The sixth subprogram VEKUT prints a vector on paper, preferably in the transposed form (line-wise). Please note that there are both a right hand side and a solution vector to print! It is therefore recommend to let this subprogram pass information on which vector is printed.
The seventh subprogram LOS solves the system of equations through a call to the provided routine SOLVE_LINEAR_SYSTEM, which is given in double precision. No changes are permitted in that routine, and it is not permitted to put it into a module!
A compulsory test example follows
33 16 72 -359 A = -24 -10 -57 b = 281 -8 -4 -17 85
Another compulsory test example is the following (with a 4 x 4 matrix)
2 3 0 0 1
0 0 1.8 10.1 11
A = b =
0.2 4.3 5 0 42
0 0.8 7 7 109
The students are required to hand in a complete program listing, and results from actual runs with matrices of the order 3, 4, 10, and 12, including input of a sparse matrix.
I assume that the main program is on the file huvud.f90, the subroutine LASMAT on the file lasmat.f90, and so on, and that a possible complete program is on the file labb5.f90.
f90 huvud.f90 lasmat.f90 lasvek.f90 ... los.f90 solve.f90
Execute with
a.out
f90 -c huvud.f90
f90 -c lasmat.f90
f90 -c lasvek.f90
...
f90 -c los.f90
f90 -c solve.f90
f90 huvud.o lasmat.o lasvek.o ... los.o solve.o
Execute with
a.out
When one routine has been changed, now only that one has to be recompiled,
followed by linking of all the routines. This method is much faster!
f90 labb5.f90
Execute with
a.out
This method is very slow!
labb5: huvud.o lasmat.o lasvek.o matin.o vekin.o \
matut.o vekut.o los.o solve.o
f90 -o labb5 huvud.o lasmat.o lasvek.o matin.o vekin.o \
matut.o vekut.o los.o solve.o
huvud.o: huvud.f90
f90 -c huvud.f90
lasmat.o: lasmat.f90
f90 -c lasmat.f90
lasvek.o: lasvek.f90
f90 -c lasvek.f90
matin.o: matin.f90
f90 -c matin.f90
vekin.o: vekin.f90
f90 -c vekin.f90
matut.o: matut.f90
f90 -c matut.f90
vekut.o: vekut.f90
f90 -c vekut.f90
los.o: los.f90
f90 -c los.f90
solve.o: solve.f90
f90 -c solve.f90
The above is used by moving the file makefile to your directory
and when you wish to compile you write only make in the
terminal window. Then only those files that have been changed
as compared with the previous make command are recompiled
(or all files if it is the first time), then all the object modules are linked
to a program, ready to run with the command labb5.
If you have used other file names you have to make the appropriate modifications to the file makefile.
In principle make works in such a way that if an item which is after a colon : has a later time than that before the colon, the command on the next line is performed.
Remark. The backslash \ indicates a continuation line in UNIX.
The routine SOLVE_LINEAR_SYSTEM is available in single precision in the course directory with the name solve1.f90 and in double precision with the name solve.f90, and looks as follows. The single precision version is discussed at length in the Solution to Exercise (11.1).
SUBROUTINE SOLVE_LINEAR_SYSTEM(A, X, B, ERROR)
IMPLICIT NONE
! Array specifications
DOUBLE PRECISION, DIMENSION (:, :), INTENT (IN) :: A
DOUBLE PRECISION, DIMENSION (:), INTENT (OUT) :: X
DOUBLE PRECISION, DIMENSION (:), INTENT (IN) :: B
LOGICAL, INTENT (OUT) :: ERROR
! The work area M is A extended with B
DOUBLE PRECISION, DIMENSION (SIZE (B), SIZE (B) + 1) :: M
INTEGER, DIMENSION (1) :: MAX_LOC
DOUBLE PRECISION, DIMENSION (SIZE (B) + 1) :: TEMP_ROW
INTEGER :: N, K
! Initiate M
N = SIZE (B)
M (1:N, 1:N) = A
M (1:N, N+1) = B
! Triangularization phase
ERROR = .FALSE.
TRIANG_LOOP: DO K = 1, N - 1
! Pivotering
MAX_LOC = MAXLOC (ABS (M (K:N, K)))
IF ( MAX_LOC(1) /= 1 ) THEN
TEMP_ROW (K:N+1 ) = M (K, K:N+1)
M (K, K:N+1) = M (K-1+MAX_LOC(1), K:N+1)
M (K-1+MAX_LOC(1), K:N+1) = TEMP_ROW (K:N+1)
END IF
IF (M (K, K) == 0.0D0) THEN
ERROR = .TRUE. ! Singular matrix A
EXIT TRIANG_LOOP
ELSE
TEMP_ROW (K+1:N) = M (K+1:N, K) / M (K, K)
M (K+1:N, K+1:N+1) = M (K+1:N, K+1:N+1) &
- SPREAD( TEMP_ROW (K+1:N), 2, N-K+1) &
* SPREAD( M (K, K+1:N+1), 1, N-K)
M (K+1:N, K) = 0 ! These values are not used
END IF
END DO TRIANG_LOOP
IF (M (N, N) == 0.0D0) ERROR = .TRUE. ! Singular matrix A
! Back substitution
IF (ERROR) THEN
X = 0.0D0
ELSE
DO K = N, 1, -1
X (K) = M (K, N+1) - SUM (M (K, K+1:N) * X (K+1:N))
X (K) = X (K) / M (K, K)
END DO
END IF
END SUBROUTINE SOLVE_LINEAR_SYSTEM
NB: The routine above uses summation of empty vectors, that is in principle SUM(vector(N+1:N)), where the vector is dimensioned to have at most N elements, that is, we have an index out of bounds. The rule for the summation routine SUM is such that in this case (sum zero elements) it will give a result zero. Compare with the DO-loop backwards. If you compile with index check, for example with f90 -C solve.f90, you may obtain an error message. I have therefore modified the routine to avoid this possibility, the modified versions are in the library (course directory).
The library is linked with
f90 prog.f90 -lnag
When the NAG library is compiled with Fortran 77, it may be necessary to use method 2 from chapter 15, that is you compile and link the necessary libraries with an implementation dependent command.
It is also helpful to use the command naghelp when available.
At the the specification of the array to store the matrix, you may chose either the method in a) or b) above, or perhaps invent a third method.
If the makefile is used, the reference to solve.f90 must be changed.
The library is linked with
f90 prog.f90 -lnagfl90
At the the specification of the array to store the matrix, you may chose either the method in a) or b) above, or perhaps invent a third method.
If the makefile is used, the reference to solve.f90 must be changed.
Write a function in Fortran with an accompanying man program for evaluating the factorial function. It is recommended to write the main program in such a way that it requests the values of the integers for which the factorial is to be evaluated. Make test runs with different integers as input.
Bessel functions are solutions to the Bessel differential equation
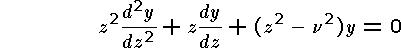
named for Friedrich
Wilhelm Bessel (1784 - 1846), who was the first to study its solutions as part
of his research in celestial mechanics. The constant v
indicates the "order" of the equation. It is possible to show that
in the case v = 0 the series
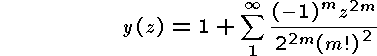
is one of the linearly independent solutions, and it is usually
denoted J0(z).
The series is convergent in the whole complex plane, but due to possible cancellation you are only requested to consider the disc | z | <= 1.
You are supposed to write a function in Fortran using single precision which evaluates J0(z) and warns the user if the argument is too large (in its absolute value), but without using any extra input or output arguments.
It is required that the function is written as generic, which means one version for complex arguments and one for real arguments, the relevant version is chosen automatically. A suitable termination criteria at the summation is when the newly added term does not contribute to the sum. The function must reside in a module, which is used by the main program described below.
Write a main program which uses the function to generate a table of J0(z) on the three lines Re(z) = -0,5; Re(z) = +0,5 and Im(z) = 0 with a suitable step size.
Computer exercise 7 b is to modify the program to handle not only single precision, but also double and quad precision. The program is to consist of modules and a main program, no other program units.
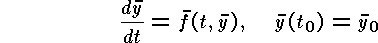
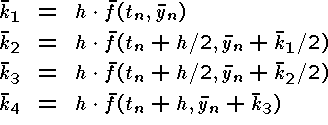
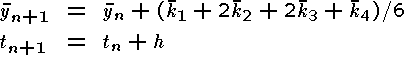
You are supposed to write a subroutine with the input parameters tn, yn, h, and f, and with the output parameters tn+1 and yn+1. Here y is a vector and f(t, y) is a vector-valued function with the scalar argument t and the vector argument y.
Apply your program on at least two of the problems below. Compute approximations to y(0.2) with using the step lengths h = 0.04; 0.02 and 0.01. Finally, a manual Richardson extrapolation is recommended.
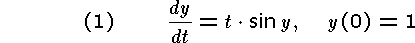
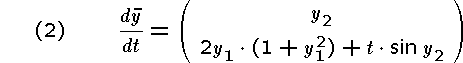
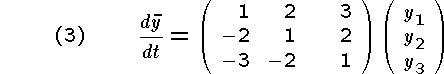
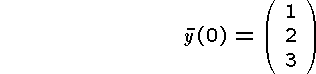
Program and the results of the execution are to be presented.
Remarks:
INTERFACE
FUNCTION F(T,Y) RESULT (FOUT)
REAL :: T
REAL, DIMENSION(:) :: Y
REAL, DIMENSION(SIZE(Y)) :: FOUT
END FUNCTION F
END INTERFACE
The program will at execution recognize the present dimension of Y and assign that same
dimension to the function F (and the result variable FOUT).
The three actual functions have to be written in a consistent way, even the first one has to be written
as a vector (with unknown length, which will evaluate to one), and not as a scalar.
My name is Bo G. Einarsson. I am a 67 years old male politician, and I live on Ekholmsvägen 249 in Linköping.
Remark:
User-defined data types are discussed in Chapter 12, section 3 and Appendix 3, section 12.
You may use a static length of all the character strings. Character strings with variable length are in an extension to the Fortran standard. At the output unnecessary spaces are not permitted. The function LEN_TRIM gives the length of a character string without its trailing blanks.
You may further assume that the used name is the first of the Christian names and there is only one extra name, which initial should be used.
If the second and optional argument is missing a default accuracy shall be used!
Also write a test program and compare with the intrinsic SIN(X). The precision may be single, double, or quad.
Expand the program to arbitrary real values of X, but no longer requiring full accuracy.
In = Integral from 0 to 1 of x^n exp(-x) dxusing the recursion formula
I0 = 1 - 1/e In = -1/e + n In-1 (n = 1, 2, 3, ...)Write the program in such a way that it uses either single or double precision, depending on a certain module defining the precision.
Look at the results and compare with simple analytical estimates!
There is a trick to evaluate these integrals correctly! Do you remember the trick? If you start with an initial value with six significant digits you may end up with a result which is pure rubbish, but if you start with a value with no significant digits at all you may end up with six significant digits in the result! Write also this program!
Your assignment is to modify this program to determine all zeroes of the function
f(x) = exp(-10x2) + cos(pi*x)
in the interval [-10; 10]. Use thereafter the method independent error estimate to verify the two roots that are smallest by magnitude.
Compile with the command
f95 -xia file.f90in order to activate the Sun interval arithmetics extensions. Further information is available on the Sun page.
I recommend that the accuracy parameters f_eps and root_eps are diminished from the present value 10-5 to be not greater than 10-10.
3.355 - ln(1.352 + cos(pi(t-0.9)/0.7))until t = 2.3 days. Its magnitude is then 2.5 until t = 4.4 days, and is then determined by the formula
3.598 - ln(1.998 + cos(pi(t-4.4)/0.4))until t = 5.2 days. Its magnitude is then 2.5 until t = 6.4 days, after which the cycle repeats with a period of 6.4 days.
Write a function which will input the value of the time t and output the brightness of the star at that time. Write a main program to print a graph of the brightness as a function of time in the interval t = 0 to t = 25.
If you do not have access to a Fortran plotting package you may use another package to plot, for example MATLAB.
WITHIN("Just testing", "test")
will return .TRUE., while
WITHIN("Just testing", "Test")
will return .FALSE.
Use one or more of the many intrinsic functions!
Test your function with a main program which inputs pairs of CHARACTER strings from the keyboard and uses the result of a function reference to cause one of the following forms of message to be displayed
The phrase 'test' is contained within "Just testing" The phrase 'Test' is not contained within "Just testing"
Use these two to write a third function to calculate the scalar triple product, defined as
[abc] = a . (b x c)
Finally write a main program which reads the three vectors a, b and c and writes the dot or scala product a . b and the vector product b x c and also the scalar triple product [abc].
Test on the following vectors:
a = ( 1 10 20 )T b = ( 5 8 9 )T c = ( 12 36 108 )Tand
a = ( 1 sqrt(2) sqrt(3) )T b = ( 5 8 9 )T c = ( 2 3 8 )Twhere sqrt means the square root (in the required precision).
Note. The vector product is defined by
c = a x b c1 = a2 b3 - a3 b2 c2 = a3 b1 - a1 b3 c3 = a1 b2 - a2 b1
u'(t) = u(t)·[A - 0.1·v(t)] + 0.015·t, u(0) = alpha v'(t) = v(t)·[0.02·u(t) - 1] + 0.0075·t, v(0) = beta
All entities are normalised, therefore the real time scale is not known, we can call the time unit "year". We indicate the number of rabbits with u(t) and the number of foxes with v(t). It is a good idea to consider the numbers as thousands!
The solution to this system of differential equations is to be programmed in Fortran, using the Runge-Kutta method and double precision. In addition to calculating the number of rabbits and foxes the program is also supposed to evaluate the error in the number of rabbits and foxes, respectively, depending on that the parameter A is not known exactly as 1 but instead only as 1 + dellta. The computations are to be performed using the values A = 1 and dellta = 0.02. The formula yo be used is
DELTAun+1 = [1 + h·(1 - 0.1·vn)]·DELTAun - 0.1·h·un·DELTAvn + h·un·dellta
DELTAvn+1 = [1 + h·(0.02·un - 1)]·DELTAvn + 0.02·h·vn·DELTAun
and
DELTAu0 = 0
DELTAv0 = 0
dellta = 0.02
It is actually using the Euler method, but you may use it for the error calculation in order to simplify the programming.
Remark: The error is called dellta because delta is a reserved name for fix point arithmetic in Ada (the original language of this exercise).
Your assignment is to run the program with two different sets of the initial values alpha (thousands of rabbits at the starting time) and beta (thousands of foxes at the starting time). These shall both be between 20 and 30.
Perform these two runs and select a suitable value of the step length h. You are in both cases supposed to go from t = 0 to t = 50.
For each case you are required to plot u ± DELTAu and v ± DELTAv as a function of t. In addition you are required to plot v as a function of u. This plot is called the phase plane.
You can either plot directly in Fortran (requires access to plotting routines), or let the Fortran program generate a file to be used by Matlab for plotting. You access for example the second column of a matrix y by writing y(:,2). One possibility is to write t, u, v, DELTAu and DELTAv as five separate vectors, which are pasted into Matlab after for example x = [, conclude with ]. As an alternative you may create a file in Fortran with a name preyandpredator.m which contains the matrix or the set of vectors to be loaded into Matlab with the command preyandpredator within Matlab. It is always wise to avoid filenames used for various actions within standard Matlab!
The command load filename.mat usually works with binary files with the extension .mat and is most suitable with files created in Matlab with the command save filename.mat. The command load filename.txt however works very well here!
alpha = beta =
alpha = beta =
