So, can the ELPA library improve upon VASP’s SCALAPACK bottleneck?
Benchmarking of the ELPA-enabled version of VASP were performed on PDC’s Lindgren (a Cray XE6) and Phase 1 of Triolith at NSC (an HP SL6500-based cluster with Xeon E5 + FDR Infiniband). For this occasion, I developed a new test case consisting of a MgH2 supercell with 1269 atoms. The structure is an experimentally determined crystal structure, but with a few per cent of hydrogen vacancies. I feel this is a more realistic test case than the NiSi-1200 cell used before. Ideally, we should see decent scaling up about 1000 cores / 64 nodes for this simulation. As usual, we expect the “EDDAV” subroutine to eventually become a dominant. The number of bands is 1488, which creates a 1488x1488 matrix that needs to be diagonalized in the bottleneck phase. Actually, this matrix size is far smaller than what ELPA was intended for, which seems to be on the order of 10,000-100,0000. So perhaps, we will not see the true strength of ELPA here, but hopefully, it can alleviate some of the pathological behavior of SCALAPACK.
Triolith
First out is Triolith, with benchmarks for 4-64 compute nodes using both 8 and 16 cores per node. I keep NPAR=nodes/2, according to earlier findings. The recommended way to run with 8c/node at NSC is to invoke a special SLURM option – that way you don’t have to give the number of cores explicitly to mpprun:
#SBATCH --ntasks-per-node 8
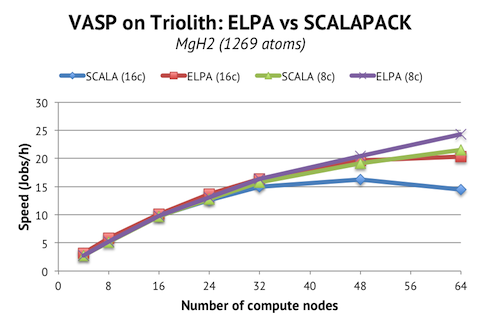
We find that the standard way of running VASP, with 16c/node and SCALAPACK, produces a top speed of about 16 jobs/h using 48 computes nodes, and going further actually degrades performance. The ELPA version, however, is able to maintain scaling to at least 64 nodes. In fact, the scaling curve looks very much like what you get when running VASP with SCALAPACK and 8c/node. Fortunately, the benefits of ELPA and 8c/node seem to be additive, meaning that ELPA wins over SCALAPACK on 48-64 nodes, even with 8c/nodes. In the end, the overall performance improvement is around 13% for the 64-node job. (While not shown here, I also ran with 96-128 nodes, and the difference there with ELPA is a stunning +30-50% in speed, but I consider the total efficiency too low to be useful.)
Lindgren
Now, let’s look at Lindgren, 8-64 compute nodes, using either 12 cores per node, or the full 24 cores. In the 12c case, I allocated three cores per socket, using
aprun -N 12 -S 3 ...
I used NPAR=compute nodes here, like before.
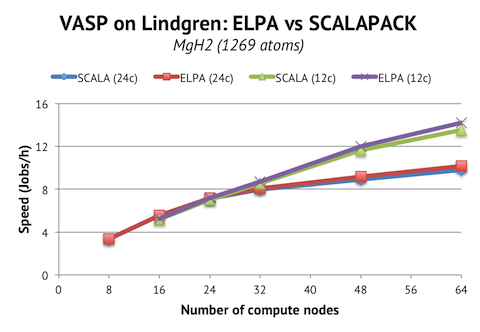
On the Cray machine, we do not benefit as much from ELPA as on Triolith. The overall increase in speed on 64 nodes is 5%. Instead, it is essential to drop down to 12c/node to get good scaling beyond 32 nodes for this job. Also, note the difference of scale on the vertical axis. Triolith has much faster compute nodes! Employing 64 nodes gives us a speed of 24.3 jobs/h vs 14.2 jobs/h, that is, a 1.7x speed-up per node or a 2.5x speed-up on a per core basis.
Parallel scaling efficiency
Finally, it is instructive to compare the parallel scaling of Lindgren and Triolith. One of the strengths of the Cray system is the custom interconnect, and since the compute nodes are also slower than on Triolith, there is potential to realize better parallel scaling, when we normalize the absolute speeds.
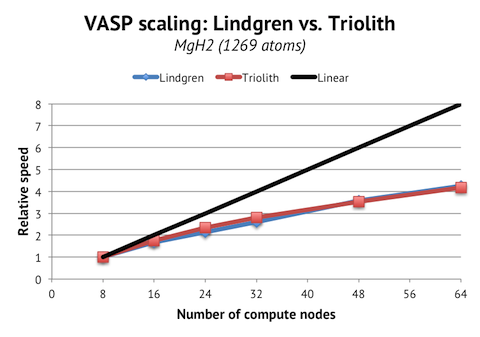
We find however, that the scaling curves are almost completely overlapping in the range where it is reasonable to run this job (4 to 64 nodes). The FDR Infiniband network is more than capable of handling this load, and the Cray interconnect is not so special at this, relatively, low-end scale.

