I promised a third round of Quantum Espresso (QE) benchmarking vs VASP, where I would try out some large supercells. Supposedly, this is where QE was supposed to shine, judging from the reported benchmarks on their home page. They show a 1500-atom system consisting of a carbon nanotube with 8 porphyrin groups attached. It shows good scaling up to 4096 cores on a Cray XT4 system.
My endeavor did not produce beautiful scaling graphs, though, as I tried several big supercells in QE with the PAW method, but were unable to get them to run reliably. They either run out of memory, or crash due to numerical instabilities. In the end, I decided to just pick the same 1532-atom carbon nanotube benchmark displayed above. It is a calculation with ultrasoft pseudopotentials, which would be unfair to compare with a VASP calculation with PAW. But since there is a special mode in VASP to emulate ultrasoft potentials, activated by LMAXPAW=-1, we can use that one make to the comparison more relevant.
In terms of numerical settings, we have 5232 electrons and the plane wave cutoff encutwfc in the QE reference calculation is 25 Ry (340 eV), with encutrho 200 Ry. The memory requirements are steep and VASP runs out of of memory on 8 nodes, but manages to run the simulation on 16 nodes, so the total memory requirement is between 256GB and 512GB. QE, on the other hand, cannot run the simulation even on 50 nodes, and it is not until I reduce encutwfc to 20 Ry and run with 50 nodes using 8 cores/node that I am able to fit in on Triolith with 32GB/node. This means that the memory requirements are significantly higher for QE than VASP. The “per-process dynamical memory” is reported as ca 1.1 GB in the output files, but in reality, it is using closer to 3 GB per process on 50 nodes.
Now, to performance results. The good news is that this system scales beautifully with VASP, but the bad news is that it does not look that great with QE. With VASP, I used no other tricks than the tried and tested NPAR=nodes, and for QE, I tested -ntg=[1-4] and used similar SCALAPACK setups (-ndiag 100 and -ndiag 196) as in the reference runs. -ntg=1 turned out to be optimal here, as expected (400-800 cores vs 500ish grid points in the z direction).
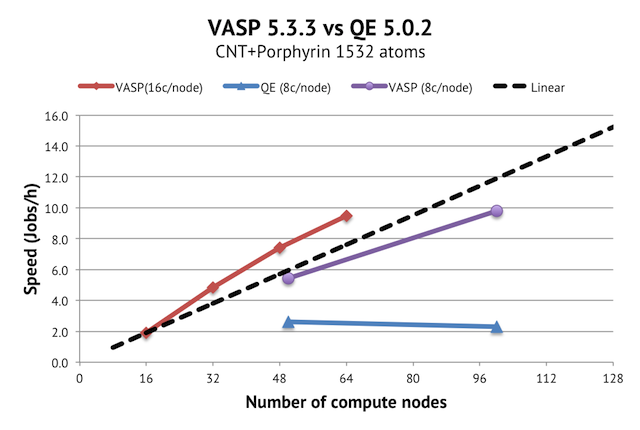
When looking at the scaling graph, we have near linear scaling in a good part of the range for VASP. It is quite remarkable that you can get ca 10 geometry optimization steps per hour on such a large system using just 4% of Triolith. This means that doing ab initio molecular dynamics on this system would be possible on Triolith, provided that you had a sufficiently large project allocation (several million core hours per month).
The high memory demands and instability of QE prevented me from doing a proper scaling study, but we have two reference points at 50 and 100 compute nodes. There is no speedup from 50 to 100 nodes. This is unlike the study on the old Cray XT4 machine, where the improvement was in the order of 1.5x going from 1024 to 2048 cores. So I am not really able to reproduce these results on modern hardware. I suspect that what we are seeing is an effect of faster processors. In general, the slower the compute node is, the better the scaling will be, because there is more work to be done relative to the communication. An alternative theory is that I am missing something fundamental in running PWscf in parallel, despite having perused the manual. Any suggestions from readers are welcome!
In conclusion, the absolute speed of Quantum Espresso using 50 compute nodes with a large simulation cell is less than half of that of VASP, which further confirms that it does not look attractive to run large supercells with QE. You are also going to need much more memory per core, which is a limitation on many big clusters today.
Update 2013-12-19: A reader asked about the effective size of the fast Fourier grids used, which is what actually matters, rather than the specified cut-of (at least for VASP). In the first results I presented, VASP actually used a 320x320x320 FFT grid vs the 375x375x375 in QE. To make the comparison more fair, I reran the data points for 50 and 100 nodes with PREC=Accurate in VASP, giving a 432x432x432 grid, which is what you are currently seeing in the graph above. The conclusion is still the same, though.
To further elaborate, I think that one of the main reasons for the difference in absolute speed (but not parallel scalability) is the lack of RMM-DIIS for matrix diagonalization in QE. In the VASP calculations, I used IALGO=48, which is RMM-DIIS only, but for QE I had to use Davidson iterative diagonalization. In the context of VASP, I have seen that RMM-DIIS can be 2x faster than Davidson for wide parallel runs, so something similar could apply for QE as well.

