OpenMX is an “order-N” DFT code with numerical pseudo-atomic basis sets and pseudopotentials. It takes a similar approach to solving the DFT problem as the SIESTA, ONETEP, and CONQUEST codes. What directed my attention towards OpenMX was a presentation at the SC13 conference showing excellent parallel scaling on the K computer, and the possibility to get very accurate solutions with the LCAO basis if necessary, as evident in the delta-code benchmark, which I wrote about earlier. It is also available under an open-source GPL license, unlike the other codes.
Installing
OpenMX is now available on Triolith. The code is written in straight C and was easy to compile and install. My changes to the makefile were:
CC = mpiicc -I$(MKLROOT)/include/fftw -O2 -xavx -ip -no-prec-div -openmp
FC = mpiifort -I$(MKLROOT)/include/fftw -O2 -xavx -ip -no-prec-div -openmp
LIB = -mkl=parallel -lifcoremt
I used the following combination of C compiler, BLAS/LAPACK and MPI modules:
module load intel/14.0.1 mkl/11.1.1.106 impi/4.1.1.036
Initial tests
To get a feel of how easy it would be work with OpenMX, I first tried to set up my trusty 16-atom lithium iron silicate cell and calculate the partial lithium intercalation energy (or the cell voltage). This requires calculating the full cell, Li in bcc structure, and a partially lithiated cell; with spin polarization. To get the cell voltage right, you need a good description of both metallic, semiconducting, and insulating states, and an all-electron treatment of lithium. The electronic structure is a bit pathologic, so you cannot expect to get e.g. SCF convergence without some massaging in most codes. For example, so far, I have been able to successfully run this system with VASP and Abinit, but not with Quantum Espresso. This is not really the kind of calculation where I expect OpenMX to shine (due to known limitations in the LCAO method), but it is a useful benchmark, because it tells you something about how the code will behave in less than ideal conditions.
With the help of the OpenMX manual, I was able to prepare a working input file without too much problems. I found the atomic coordinate format a bit too verbose, e.g. you have to specify the spin up and spin down values for each atom individually, but that is a relatively minor point. As expected, I immediately ran into SCF convergence problems. After playing around with smearing, mixing parameters and algorithms, I settled with the rmm-diisk algorithm with a high Kerker factor, long history, and 1000K electronic temperature. This lead to convergence in about 62 SCF steps. For comparison, with VASP, I got convergence in around 53 SCF steps with ALGO=fastand linear mixing. From the input file:
scf.Mixing.Type rmm-diisk
scf.maxIter 100
scf.Init.Mixing.Weigth 0.01
scf.Min.Mixing.Weight 0.001
scf.Max.Mixing.Weight 0.100
scf.Kerker.factor 10.0
scf.Mixing.StartPulay 15
scf.Mixing.History 30
scf.ElectronicTemperature 1000.0
The choice of basis functions is critical in OpenMX. I recommend the paper by M. Gusso in J. Chem. Phys. for a detailed insight into the quality of the OpenMX basis set vs plane-waves. From quantum chemistry codes, I know that double-zeta basis will get you qualitatively correct results, but triple-zeta basis and above is required for quantitative results. It also seems imperative that you always have at least one d-component. I tried three combinations: s2p1+d (SVP quality), s2p2d1+f (DZP quality), and s3p3d3+f (TZP quality). The resulting cell voltages are shown below. The voltages are expected to decrease as the basis set size increases due overbinding from basis set superposition errors.
s1p1+d: 3.85 V
s1p1+d: 3.40 V (counterpoise correction)
s2p2d1+f: 3.14 V
s2p2d1+f: 3.00 V (counterpoise correction)
s3p3d3+f: 2.77 V (counterpoise correction)
For comparison, the converged VASP result with 550 eV and PREC=accurate is 2.80 V, meaning that the s3p3d3-level calculation is quite accurate. This confirms the delta-code benchmark study, where OpenMX calculations were shown to be as accurate as those of VASP, provided that a big basis set is used. In terms of speed, however, the results are not that impressive, on one Triolith compute node with 16 cores, VASP runs this 16-atom cell in 18 seconds at 500eV, whereas OpenMX with s3p3d3 basis takes 700 seconds! We will see, however, in the next section, that the outcome is different for large systems.
512-atom carbon nanotube
I think that carbon nanotubes (and other nanostructures) are a better fit for order-N approaches. For this purpose, I set up a (16,0) nanotube with 512 atoms including terminating hydrogens. It is stated in the OpenMX manual that you need at least 1 atom per MPI process, so ideally we could scale up to 512 cores with MPI, and possibly more with OpenMP multithreading.
Here, I choose DZP level basis set for OpenMX:
<Definition.of.Atomic.Species
C C6.0-s2p2d1 C_PBE13
H H6.0-s2p2d1 H_PBE13
Definition.of.Atomic.Species>
I believe that this is a slightly weaker basis set than what you would get in a standard VASP approach, so for the corresponding VASP calculation, a “rough” basis set of ENCUT=300 and PREC=Normal was chosen. For reference, the ENMAX value in the carbon POTCAR is 400 eV, which is what you would normally use. The calculations are spin-polarized. OpenMX reaches SCF convergence in 46 cycles using a similar scheme as above, and the VASP calculation converges in 34 cycles with the standard ALGO=fast. Both programs agree on a magnetic moment of 9.5-10.0.
In terms of performance, regular order-N(3) DFT in OpenMX is about as fast as in VASP, at least for wider parallel jobs:
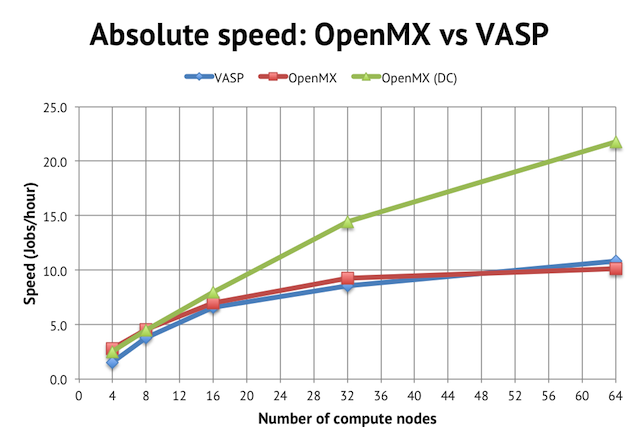
We reach a peak speed of about 10 jobs/hour (or 10 geometry optimization steps per hour) on NSC’s Triolith. Interestingly, for the narrowest job with 4 compute nodes, OpenMX was almost twice as fast as the corresponding VASP calculation, implying that the intra-node performance is very strong for OpenMX, perhaps due to the use of hybrid OpenMP/MPI. Unfortunately, the calculation runs out of memory on less than 4 compute nodes, so I couldn’t test anything smaller (see more below).
The main benefit of using OpenMX is, however, the availability of linear scaling methods. The green line in the graph above shows the speed achieved with the order-N divide-conquer method (activated by scf.EigenvalueSolver DC in the input file). It cuts the time to solution by half, reaching more than 20 jobs/hour, but please note that the speed for narrow jobs is the same as regular DFT, so the main strength of the DC method seems not to be in improving serial (or intra-node performance) but rather in enabling better parallel scaling.
The impact on parallel scalling is more evident if we normalize the performance graph to relative speeds vs the 4-node jobs:
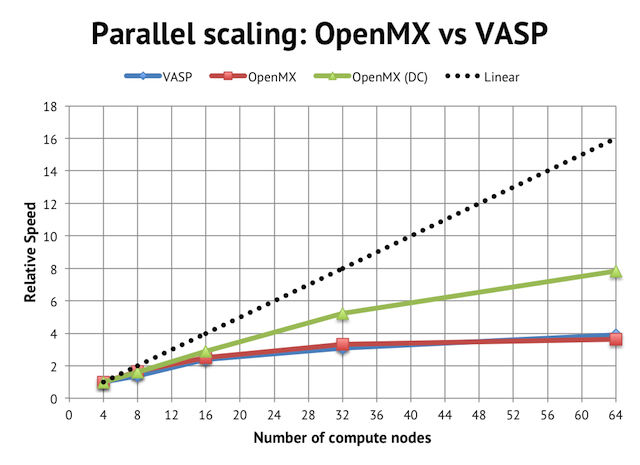
Regular DFT in VASP and OpenMX flattens out after 16 compute nodes, which is equivalent to 256 cores in total or 2 atoms/core, whereas with the linear scaling method, it is possible to beyond that.
Memory consumption
The main issue I had with OpenMX was memory consumption. OpenMX seems to replicate a lot of data in each MPI rank, so it is essential to use the hybrid MPI/OpenMP approach to conserve memory. For example, on 4 compute nodes, the memory usage looks like this for the calculation above:
64 MPI ranks without OpenMP threads = OOM (more than 32 GB/node)
32 MPI ranks with 2x OpenMP threads = 25 GB/node
16 MPI ranks with 4x OpenMP threads = 17 GB/node
8 MPI ranks with 8x OpenMP threads = 13 GB/node
with 2x OpenMP giving the best speed. For wider jobs, 4x OpenMP was optimal. This was a quite small job with s2p2d1 basis and moderate convergence settings, so I imagine that it might be challenging to run very accurate calculations on Triolith, since there is only 32 GB memory in most compute nodes.
Of course, adding more nodes also helps, but the required amount of memory per node does not strictly decrease in proportion to the number of nodes used:
4 nodes (2x OpenMP) = 25 GB/node
8 nodes (2x OpenMP) = 21 GB/node
16 nodes (2x OpenMP) = 22 GB/node
32 nodes (2x OpenMP) = 18 GB/node
So when you are setting up an OpenMX calculation, you need to find the right balance between the number of MPI ranks and OpenMP threads in order to get good speed without running out of memory.
Conclusion
In summary, it was a quite pleasant experience to play around with OpenMX. The performance is competitive, and there is adequate documentation, and available example calculations, so it is possible to get started without a “master practitioner” nearby. For actual research problems, good speed and basic functionality is not enough, though, as usually, you need to be able to calculate specific derived properties, and visualize the results in a specific way. I noticed that there are some post-processing utilities available, even inside OpenMX itself, and among the higher level functionality, there is support for relativistic effects, LDA+U, calculation of exchange coupling, electronic transport, NEB and MLWFs, so I think many of the modern needs are, in fact, satisfied.

